Z minulého dílu víme, jak AI funguje, vytvořili jsme si velice jednoduchou lineární regresi k predikci cen automobilů. Nicméně, obvykle se u AI setkáváme s pojmem neuronové sítě (neural networks), o kterých bude tento, již šestý díl seriálu.
Obsah
Teorie
Neuronová síť (NN)
Stejně jako lineární regrese, i neuronové sítě jsou jedním z modelů pro AI. Správně by se mělo říkat umělá neuronová síť (ANN – artificial neural network), protože neuronovou síť nalezneme u každého z nás v hlavě, ale obvykle se to zkracuje, jakmile se mluví o AI.
Neuronová síť je nejvíce využívaným druhem AI, protože se nejvíce podobá lidskému myšlení a dokáže najít různé, složité souvislosti ve velkých datech – obdobně jako to dělá náš mozek, aniž bychom o tom více věděli.
Princip
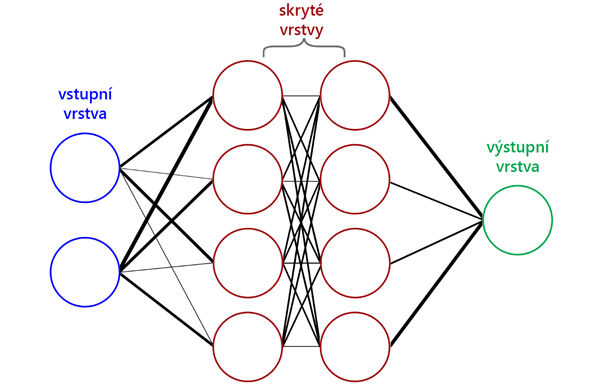
Neuronové sítě se obvykle znázorňují pomocí zjednodušených schémat jako je na obrázku.
Každý kruh označuje jeden samostatný neuron (ten si představte jako libovolné reálné číslo mezi 0 a 1 včetně – v odborné literatuře se to označuje jako aktivace daného neuronu). Každá čára spojuje přesně dva neurony – tento spoj se nazývá synapse a má určitou váhu (weight). Každý spoj je různě významný (čím vyšší je váha, tím významnější je) – na obrázku znázorněno pomocí tloušťky jednotlivých čar.
Rozlišujeme dva typy NN podle jejich spojení:
- fully-connected – kde je každý neuron jedné vrstvy spojen se všemi neurony další vrstvy (ten jsem použil na obrázku)
- sparse-connected – kde není každý neuron jedné vrstvy spojen se všemi neurony další vrstvy
Každá NN musí mít vstupní a výstupní vrstvu o libovolném počtu neuronů (na obrázku jsou dva vstupní neurony – modré, a jeden výstupní – zelený). U složitějších / komplexnějších problémů najdeme také jednu až několik vrstev skrytých (na obrázku červeně) – skryté se jim říká proto, že jejich výsledek není přímo výsledkem NN. Jakmile máme skrytých vrstev hodně, mluvíme o tzv. deep neural network.
Důležité je také zmínit, že počet neuronů a vrstev v schématu a v realitě se může lišit. Zjednodušuje se to proto, že často NN mají na vstupu i několik set až tisíc neuronů a schéma by pak bylo zbytečně obrovské.
Experiment
V experimentu níže budeme mít sadu obrázků s rozlišením 28×28 pixelů. Na nich jsou ručně psaná čísla od 0 do 9 a cílem NN bude přiřadit ke každému obrázku „nálepku“ podle čísla, které na něm je, a následně určit relativní přesnost.

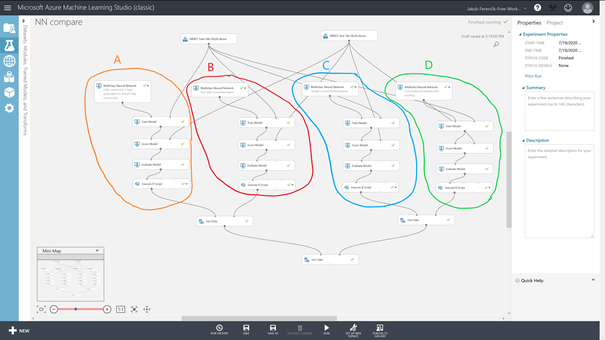
Celý experiment v Azure MLS bude vypadat následovně:
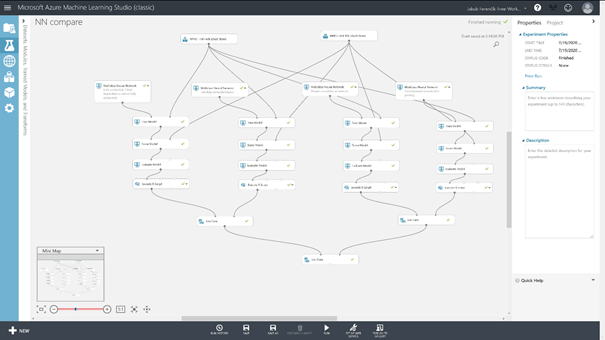
Na první pohled se může zdát příliš komplikovaný, ovšem pokud se podíváte podrobněji, zjistíte, že to jsou čtyři téměř totožné části spojené dohromady. Síť rozdělíme na čtyři části:
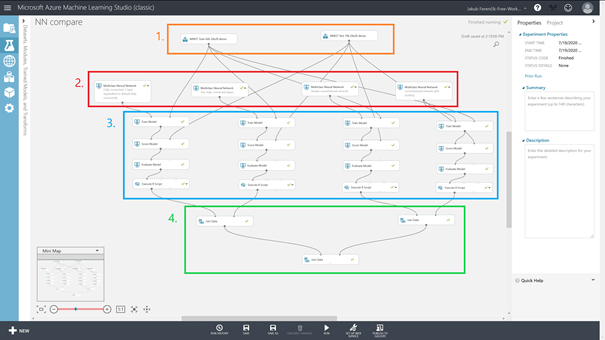
Pro potřeby tohoto dílu jsem spojil čtyři jednotlivé NN (označené jako A, B, C, D) do jednoho experimentu:
V 1. části pouze importujeme dva MNIST datasety, které obsahují 60 tisíc, resp. 10 tisíc obrázků ručně psaných čísel s „nálepkou“.
Z pohledu tohoto dílu seriálu bude 2. část tou nejzajímavější, a hlavně úplně novou. Jednotlivé bloky obsahují různé nastavení NN, které si projdeme později v tomto díle.
S bloky v 3. části jsme se již seznámili v minulých dílech, a proto se jimi nebudeme zabývat.
A v poslední 4. části, pouze sjednotíme výsledky různých NN do jednoho výsledného datasetu pro přehlednost.
Tyto NN si můžete uložit jako jednotlivé experimenty do svého Workspace z následujících odkazů:
NN A – https://gallery.azure.ai/Experiment/4b8f1f17e02d4b9ca60486fd56c0fba6
NN B – https://gallery.azure.ai/Experiment/b5aa6d21e8b24357a9dae21a5b05bfaf
NN C – https://gallery.azure.ai/Experiment/5c93ce4cf5924d349df42593a4da8928
NN D – https://gallery.azure.ai/Experiment/7d3f74981b5b42cd9687370671c86696
Každá z následujících NN má ve vstupní vrstvě 784 neuronů (pro každý pixel obrázku 1 – tj. 28×28) a 10 neuronů ve výstupní vrstvě (tj. pravděpodobnosti pro jednotlivá čísla 0-9). Liší se však počtem skrytých vrstev a uspořádáním.
Multi-class Neural Network
Neuronová síť A
Tato NN je tou nejjednodušší ze všech v experimentu, má pouze 1 skrytou vrstvu, která je tvořena 100 neurony. Ze všech 4 různých NN je tato tou nejméně přesnou, ale zato tou nejrychlejší. S přesností se dostáváme na skvělých 97,75 % (resp. relativní chyba je 2,25 %), jak můžete vyčíst z obrázku níže.
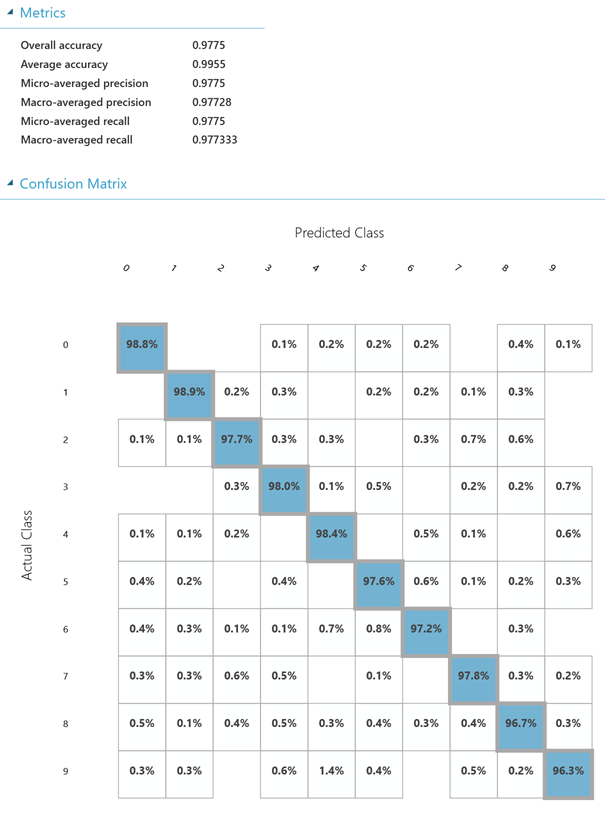

Neuronová síť B
Pokud zvýšíme počet skrytých vrstev na dvě a počet skrytých neuronů na 200 (v každé vrstvě), umožníme NN najít mnohem komplexnější souvislosti a díky tomu i zajistit lepší výsledky. Přesnost se nám zvýší na 98,1 % (relativní chyba je 1,9 %).
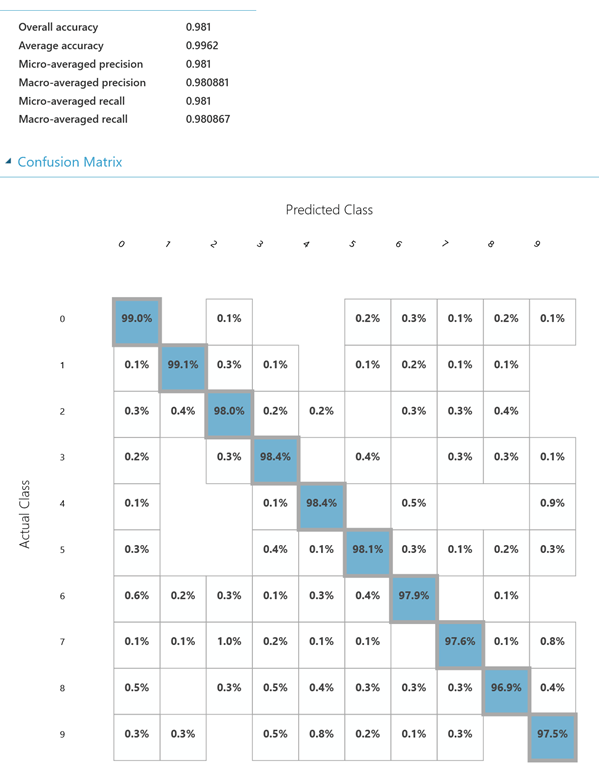

Neuronová síť C
Tentokrát již nebudeme navyšovat počty skrytých vrstev a neuronů jako u NN B, ale použijeme trochu matematiky, abychom se dostali k ještě přesnějším výsledkům. Tou matematickou operací bude tzv. konvoluce. Co to znamená? Každý konvoluční neuron v síti se zabývá pouze svou určitou oblastí (tzv. receptivním polem), pro kterou se vyhodnocuje jeho aktivační funkce. Představte si to třeba na obrázku – když uděláme z originálního velkého obrázku výřez, může to představovat receptivní pole. Jakmile nějaká NN obsahuje konvoluci, říkáme těmto sítím CNN (resp. ConvNet, Convolutional Neural Network). S přesností se zde dostáváme na 98,41 % (relativní chyba je 1,59 %).
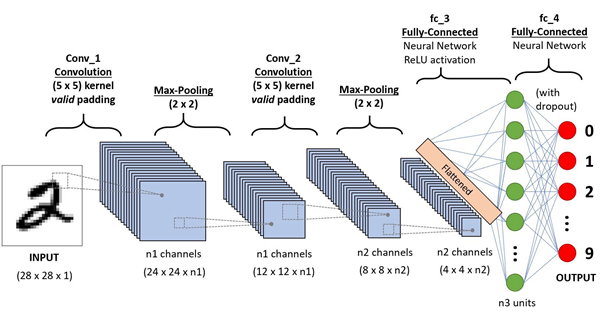
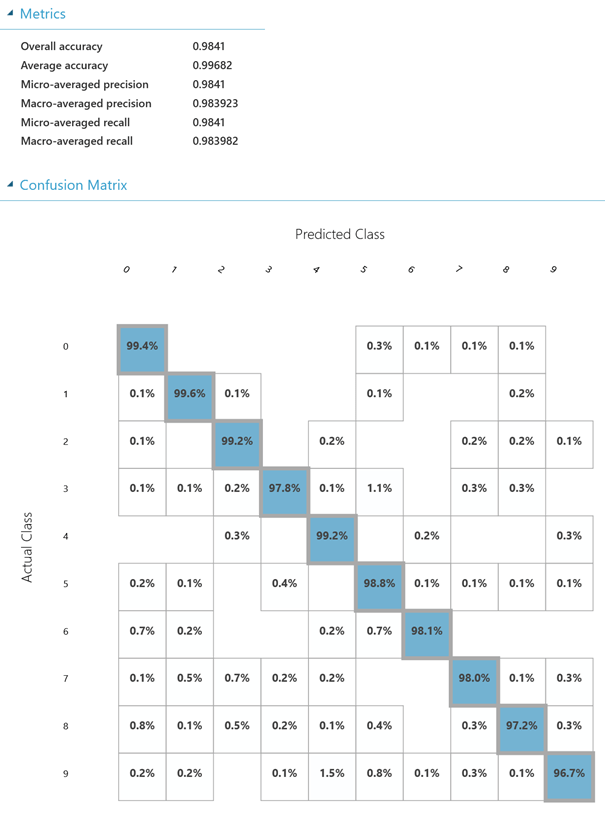

Neuronová síť D
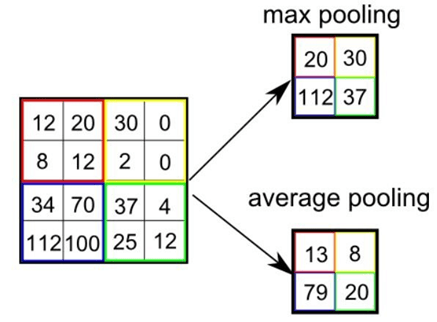
Konvolucí ovšem naše možnosti nekončí, ještě tu máme tzv. max-pooling (maximální sdružování). Max-pooling nám umožňuje z neuronových shluků dostat pouze jeden neuron (čímž se zmenší počet neuronů pro výstupní vrstvu) a to buď na základě maximální hodnoty ze shluku (max-pooling), který se používá nejčastěji, nebo na základě průměru z hodnot ve shluku (average pooling). Pro nás bude tento typ NN (sdružovací konvoluční neuronová síť) tím nejpřesnějším, avšak také nejpomalejším – training může trvat až hodinu. Přesnost zde dosahuje již pěkných 98,83 % (relativní chyba je 1,17 %).
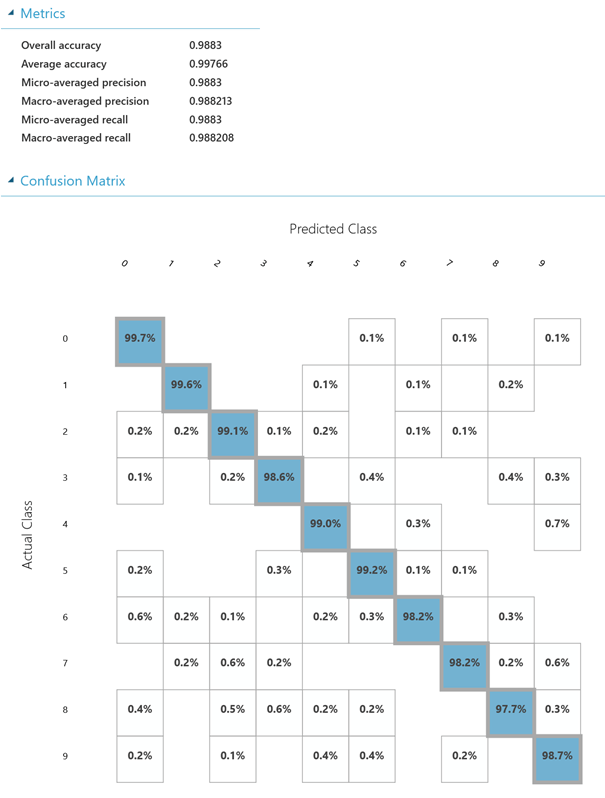

Závěr
V tomto díle seriálu jste se seznámili s trochu pokročilejší částí neuronových sítí. Podívali jsme se na základní teorii, která za neuronovými sítěmi stojí. Proč základní? Protože k pochopení AI je prvně potřeba pochopit matematiku vysokoškolské úrovně, jelikož pomocí ní se všechno definuje – pokud to přesto chcete zkusit, podívejte se na videa od 3b1b, které naleznete níže. Můžete se podívat i na ostatní videa, které vám mohou pomoct lépe pochopit neuronové sítě, díky propracovaným animacím a ucelenému výkladu.
Doporučená videa
Welch labs: https://www.youtube.com/playlist?list=PLiaHhY2iBX9hdHaRr6b7XevZtgZRa1PoU
giant_neural_network: https://www.youtube.com/playlist?list=PLxt59R_fWVzT9bDxA76AHm3ig0Gg9S3So
3b1b: https://www.youtube.com/playlist?list=PLZHQObOWTQDNU6R1_67000Dx_ZCJB-3pi
Microsoft STC – Erik Stoklasa: https://www.youtube.com/watch?v=Ji6IleR1Lmo