Excel je program známý všem studentům. Kolik z vás jej ale používá k řešení školních úkolů do matematiky? Tento článek vám ukáže, jak v Excelu počítat a zobrazovat matematické funkce, jako jsou například lineární, kvadratické nebo logaritmické.
V dnešním příspěvku si ukážeme, jak si spojit látku vyučovanou ve středoškolské matematice se znalostí Excelu. Tématem tohoto článku, v pořadí již druhého, jsou funkce. Můžete se podívat na první díl, který se věnuje především základním aritmetickým operacím.
Lineární funkce
Předpis lineární funkce, který naleznete v matematických tabulkách, je y = ax + b.
Velikost čísla a ovlivní odchylku přímky od os souřadnic. Pokud je a kladné, graf bude rostoucí. Kdyby bylo naopak záporné, zapříčiní, že graf bude klesat. Pokud je a větší než 1, rostoucí funkce poroste rychleji (a klesající bude rychleji klesat).
Číslo b, které přičítáme k x, udává posunutí funkce. Pokud je číslo kladné (jako například +1) posune se graf o jedno nahoru, protne tedy svislou osu y v bodě [0;1]. Záporné číslo (jako třeba -1) způsobí, že průnik s osou y se posune do bodu [0;-1].
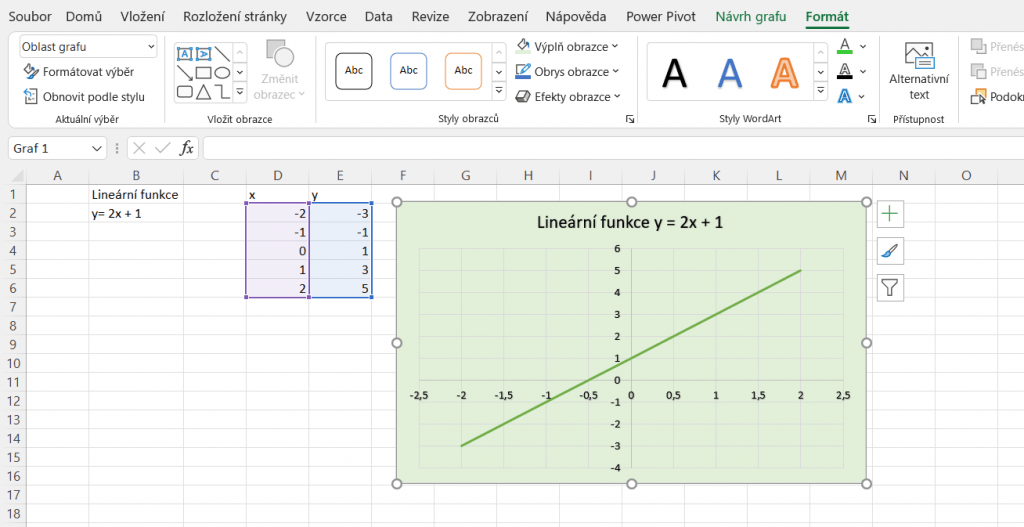
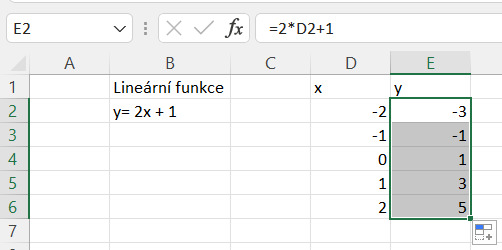
Rozhodli jsme se vytvořit lineární graf s předpisem y = 2x + 1. Už teď tedy víme, že funkce je rostoucí a posunutá o jedna nahoru. Pro vytvoření grafu jsme do jednoho sloupečku v excelu zadali hodnoty na ose x, které chceme mít v grafu vykresleny. Do vedlejšího sloupce y jsme zadali vzorec = 2 * (souřadnice vedlejší buňky) + 1 a potažením pravého dolního rohu buňky jsme rozšířili sloupec tak, aby se nám vypočítaly zbývající hodnoty y pro dané x.
Pro vytvoření grafu této lineární funkce jsme myší označili našich celkem 10 hodnot a na kartě Vložení pod oddílem Grafy vybrali vhodný graf. Pro funkci je nejvhodnější bodový graf, vykreslujeme totiž závislost jedné veličiny na druhé.
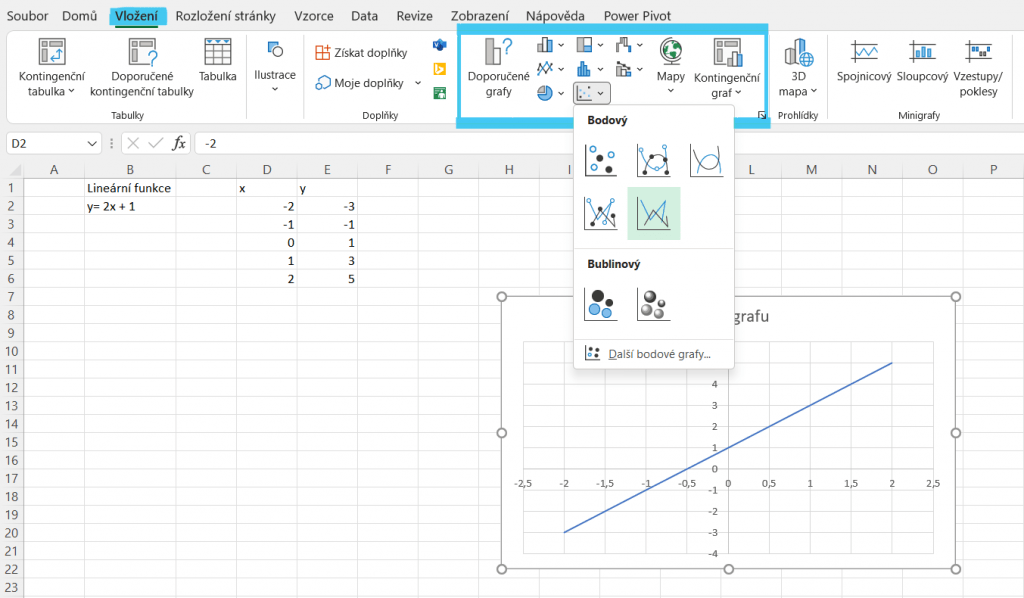
Když máme graf aktivní, zobrazí se nám v pásu karet další dvě možnosti: Návrh grafu a Formát. S jejich pomocí si můžeme s naším výsledkem pohrát jako třeba vybrat jiné barvy a efekty nebo zdůraznit určité důležité hodnoty.
Kvadratické funkce
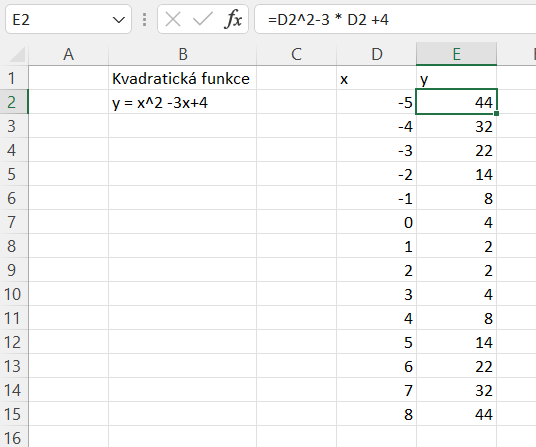
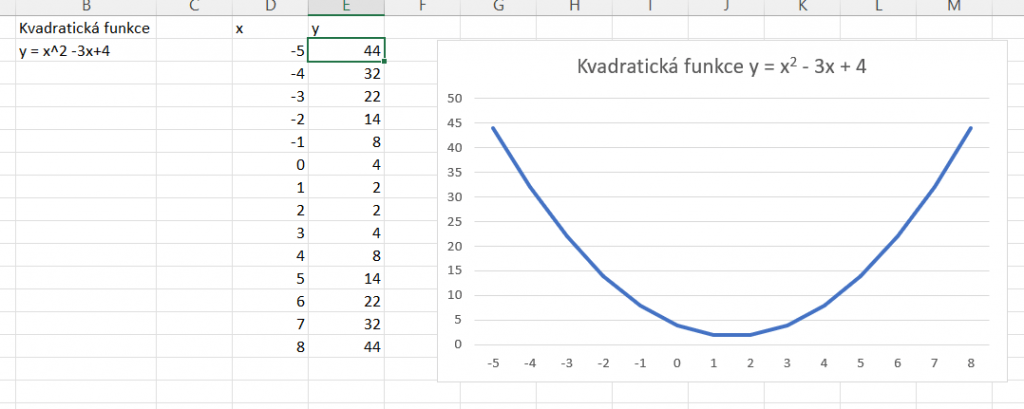
U tvorby grafů kvadratických funkcí budeme postupovat podobně jako u lineárních. Předpisem kvadratické funkce je y = ax2 + bx + c. Zatímco grafem lineární funkce byla přímka, u kvadratické to bude parabola.
Exponenciální funkce
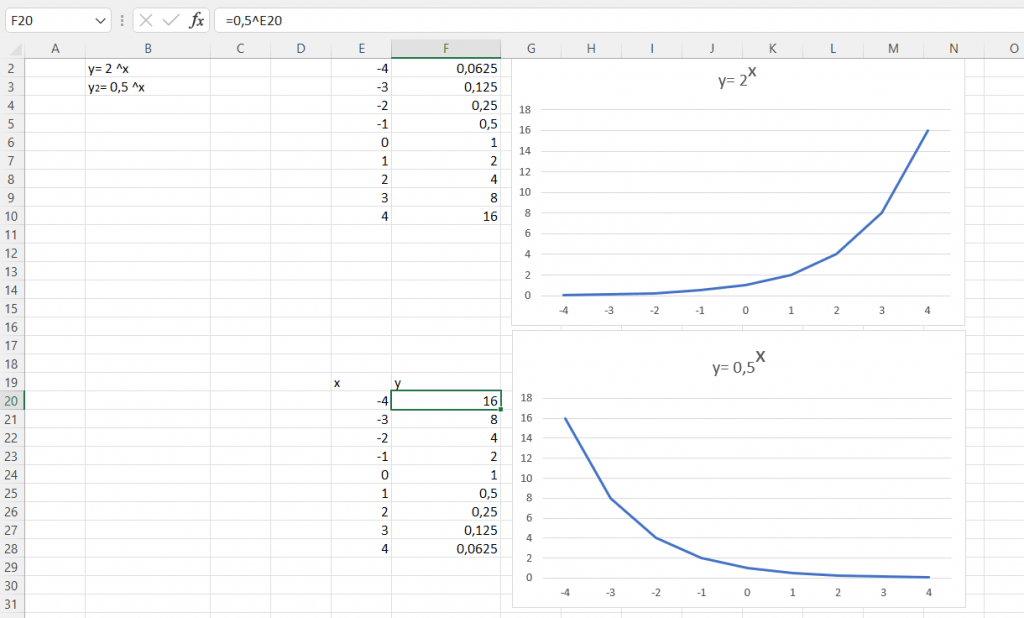
Základní předpis exponenciální funkce zní y = aˆx. Základ a nesmí být roven jedné nebo nule. Vznikla by totiž konstantní funkce. Také máme podmínku, že se musí základ nacházet v intervalu kladných čísel. Existují dva scénáře, jak bude funkce vypadat. Pokud bude základ a v intervalu (0, 1), funkce bude klesat. Rostoucí exponenciální funkce nastane tehdy, když se bude základ nacházet v intervalu (1, ∞).
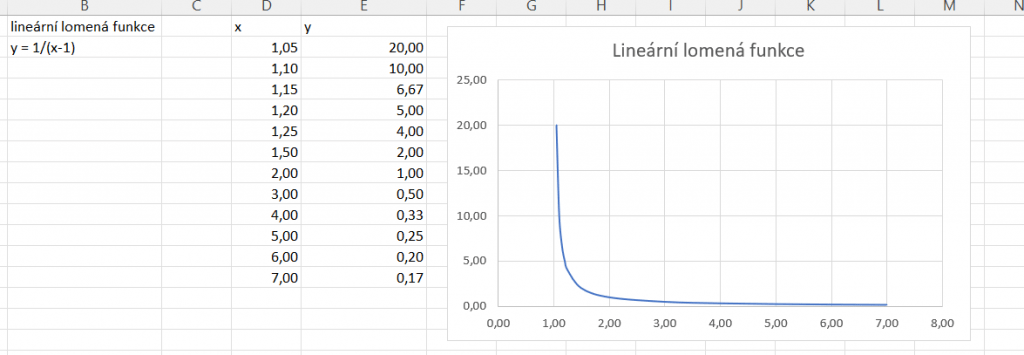
Lineární lomená funkce
Předpis lineární lomené funkce je trochu složitější, máme totiž nově neznámou i ve jmenovateli. Obecný předpis zní y = (ax + b)/(cx + d). Grafem funkce je hyperbola.
Logaritmické funkce
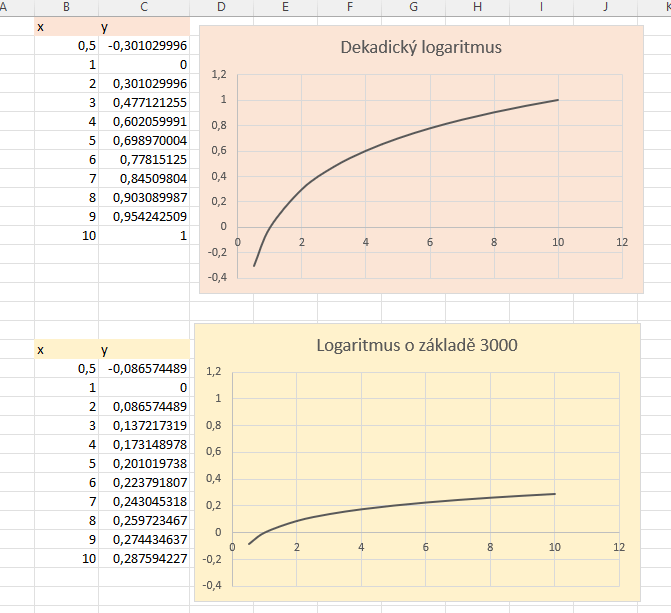
Výpočtům logaritmické funkce jsme se již trochu věnovali v minulém díle. Pro výpočet dekadického logaritmu čísla x je vhodné použít funkci =LOG() s číslem x v závorce. Funkce =LOGZ() s jedním parametrem v závorce také vrátí hodnotu dekadického logaritmu zadaného čísla. V případě, že chceme počítat logaritmus o jiném základu, zadáme do závorky funkce =LOGZ() čísla dvě: nejprve hodnotu čísla, jehož logaritmus chceme vypočítat, poté středník následovaný hodnotou základu počítaného logaritmu.
V ukázce jsme pro porovnání použili obě funkce. Přiřadili jsme oběma stejné hodnoty x, ale různé základy. Oranžová funkce znázorňuje logaritmus o základu 10, žlutá funkce ukazuje logaritmus o základu 3000.
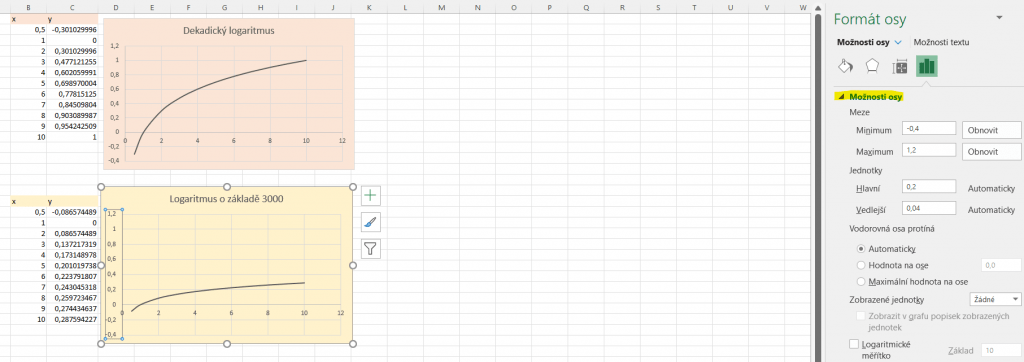
Abychom grafy mohli porovnat, museli jsme upravit popisky os, aby souhlasily. Při kliknutí na hodnoty na jedné z os se vpravo zobrazí pás s názvem Formát osy. V sekci Možnosti osy nastavíme minimum a maximum tak, aby souhlasilo s druhým grafem a abychom mohli srovnat rozdíly v zakřivení obou funkcí. Díky tomu můžeme říct, že logaritmus o základu 3000 roste pomaleji než logaritmus o základu 10.
Ještě lepší pro porovnávání dvou či více grafů je logaritmické měřítko, které můžeme nastavit také v oddíle možnosti osy.
Goniometrické funkce
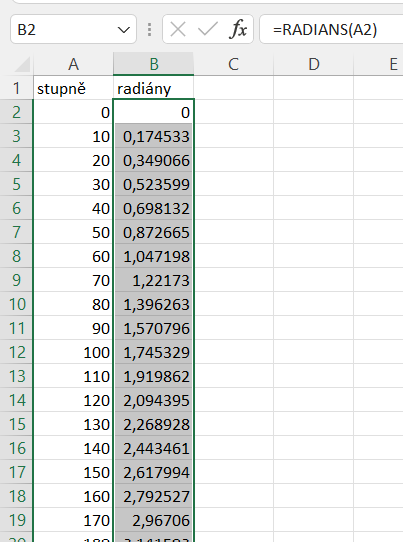
Trochu jiné bude počítání a vytváření grafů goniometrických funkcí. Jedná se totiž o periodické funkce, jejichž průběh se vždy zopakuje po určitém intervalu. Funkce, které budeme pro výpočet používat, požadují zadání hodnot v radiánech. Na to můžeme použít funkci =RADIANS(), která čísla ze stupňů na radiány převede.
Sinus a kosinus
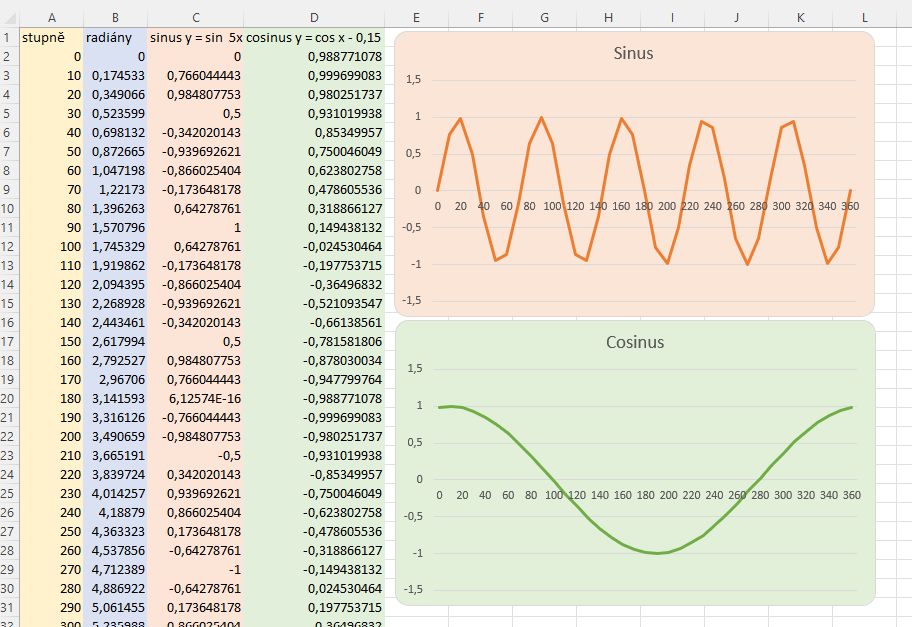
Nyní už můžeme přejít k samotnému výpočtu. Funkce, které nám pomůžou, budou =SIN() a =COS(). Nesmíme zapomenout dosadit hodnotu v radiánech, a poté vytvoříme graf. Tady si musíme dávat pozor.
Pokud bychom pro vytvoření grafu označili sloupeček s radiány a s vypočtenými hodnotami funkcí sinus a kosinus, mnoho bychom se z grafu nedozvěděli. Na ose x by totiž byly místo stupňů radiány. Proto musíme označit jak sloupeček se stupni, tak s vypočtenými hodnotami funkcí. Sloupeček s radiány pro vytváření grafu nepotřebujeme, slouží nám pouze k výpočtu hodnot.
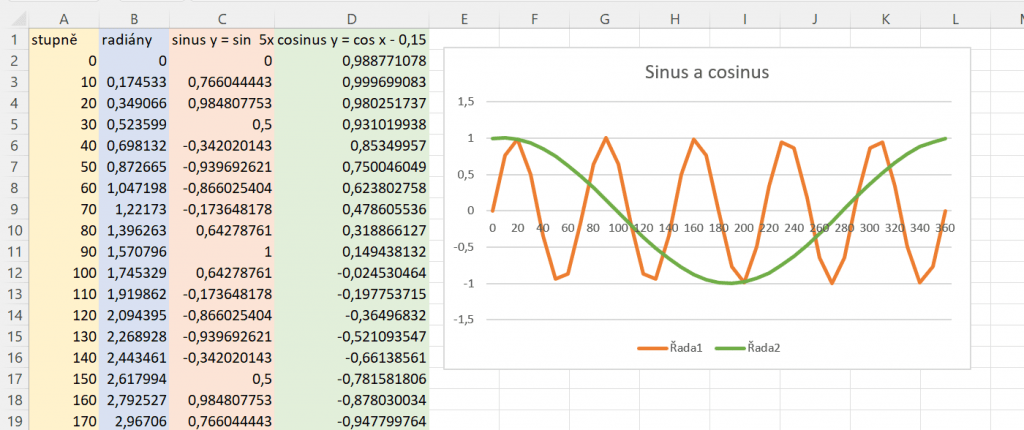
Pokud chceme mít funkce zkombinované v jednom grafu, nejvíce se hodí spojnicový graf. Vytvoříme jej označením sloupce se stupni, obou sloupců s výpočty zároveň a zvolením patřičného grafu na kartě Vložení.
Tangens a kotangens
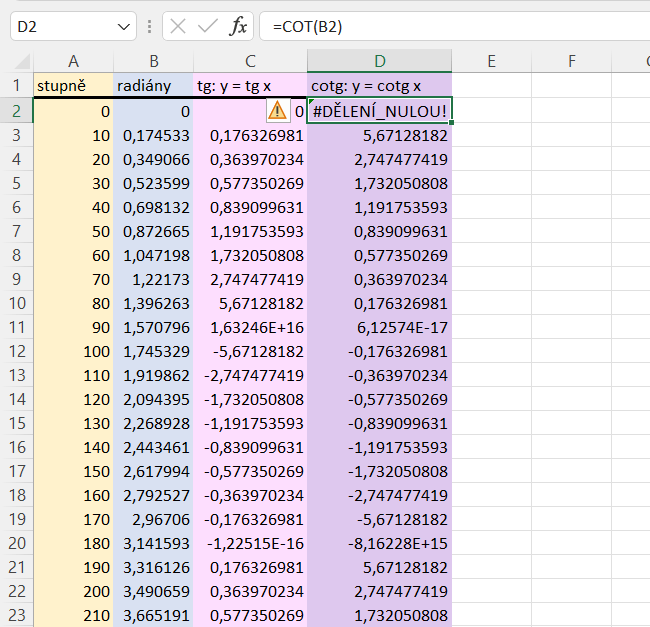
Podobně, jako jsme to udělali před chvílí, můžeme při výpočtu hodnot funkcí tangens a kotangens využít =TG() a =COT(). Tyto funkce nám během vteřiny spočítají hodnoty, ke kterým bychom jen těžce došli sami.
Kombinovaný graf
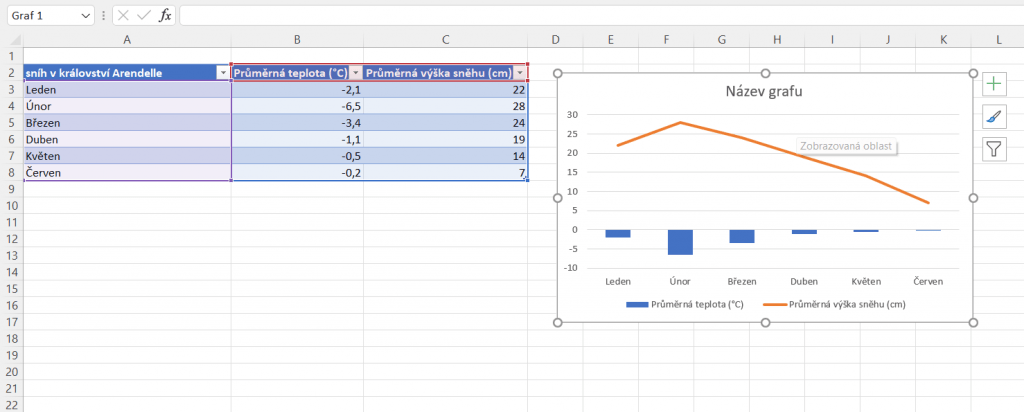
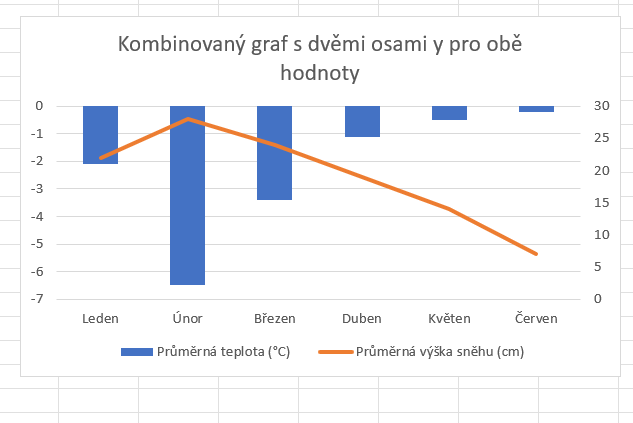
Kombinovaný graf slouží k vynesení a znázornění různých hodnot do jednoho grafu. Tyto hodnoty bychom navzájem obtížně srovnávali, obzvlášť, když se jedná o veličiny s rozdílnými jednotkami. Často bychom také pro každou použili jiný typ grafu. V našem fiktivním příkladu se jedná o srovnání průměrných teplot vzduchu a výšky sněhu v různých měsících.
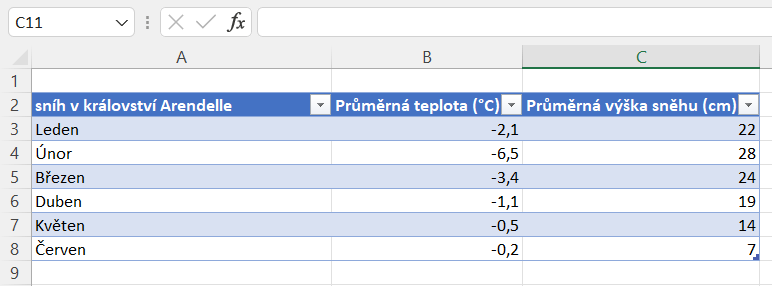
Po vytvoření tabulky vše označíme a na kartě Vložení zvolíme kombinovaný graf. Pokud vše uděláme správně, výsledkem bude graf, který v sobě pojí dva různé typy. U nás je to např. spojnicový a sloupcový. V tomto kroku zkontrolujeme, zda vše odpovídá a zda se naše hodnoty netransformovaly někam, kde být nemají.
To ale není všechno. Graf jsme sice vložili správně, ale naše práce tím nekončí. Bez správné úpravy os totiž není vůbec poznat, co má graf znázorňovat. Osa y zde znázorňuje hodnoty dvou různých veličin. Graf upravíme, aby obsahoval osu y pro každou veličinu zvlášť.
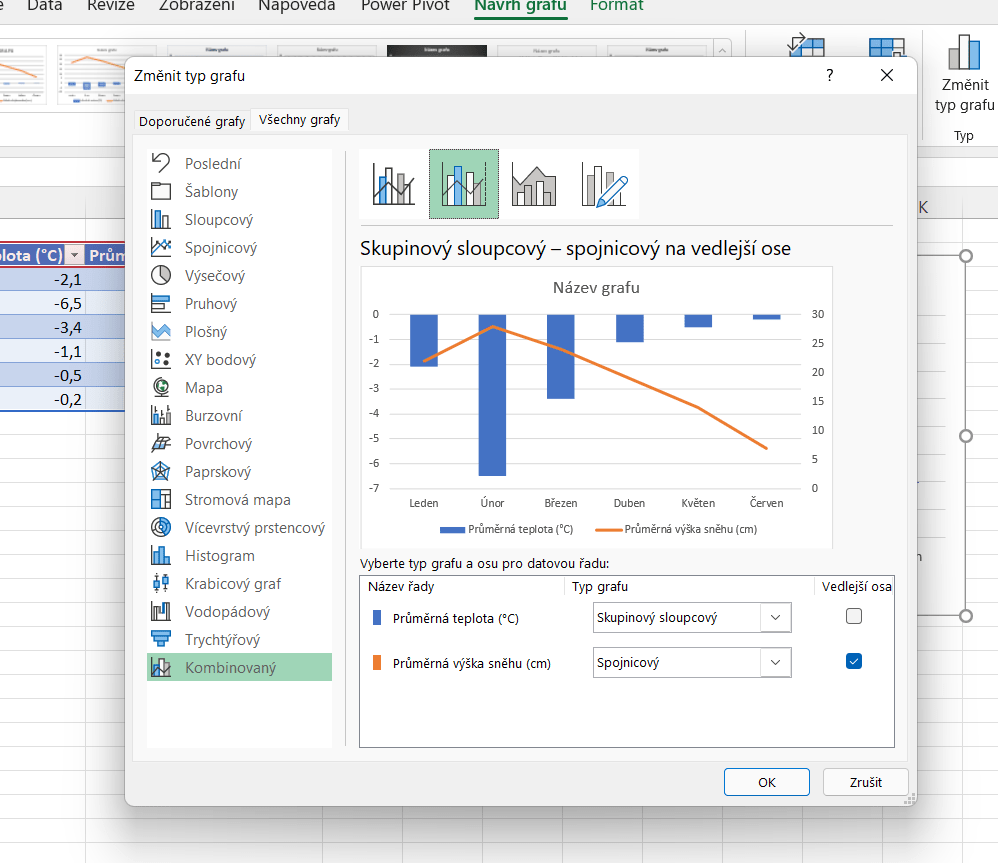
Na kartě Návrh grafu klikneme na Změnit typ grafu. Pro vložení druhé osy y vybereme v nově otevřeném okně možnost Skupinový sloupcový – spojnicový na vedlejší ose. Ve spodní části okna zatrhneme políčko u té řady, kterou chceme mít na vedlejší ose (osa vpravo). Poté potvrdíme tlačítkem OK.
Závěr
V tomto článku jsme se zaměřili především na výpočet hodnot funkcí a tvorbu jejich grafů. Věříme, že nově nabyté znalosti využijete třeba v hodinách matematiky nebo fyziky.